Matplotlib¶
Matplotlib is a python 2-d plotting library which produces publication quality figures in a variety of formats and interactive environments across platforms. Matplotlib can be used in Python scripts, the Python and IPython shell, web application servers, and six graphical user interface toolkits.
Documentation¶
The matplotlib documentation is extensive and covers all the functionality in detail. The documentation is littered with hundreds of examples showing a plot and the exact source code making the plot:
- Matplotlib home page: key pylab plotting commands in a table.
- Matplotlib manual
- Thumbnail gallery: hundreds of thumbnails linking to the source code used to make them (find a plot like the one you want to make).
- Code examples: extensive examples showing how to use matplotlib commands.
Hints on getting from here (an idea) to there (a plot)¶
- Start with Screenshots section of the manual for a broad idea of the plotting capabilities
- Most of the high-level plotting functions are in the pyplot module and you can find them quickly by searching for pyplot.<function>, e.g. pyplot.errorbar.
Pylab and Pyplot and NumPy
Let’s demystify what’s happening when you use ipython --pylab and clarify the relationship between pylab and pyplot.
matplotlib.pyplot is a collection of command style functions that make matplotlib work like MATLAB. This is just a package module that you can import:
import matplotlib.pyplot
print sorted(dir(matplotlib.pyplot))
Likewise pylab is also a module provided by matplotlib that you can import:
import pylab
This module is a thin wrapper around matplotlib.pylab which pulls in:
- Everything in matplotlib.pyplot
- All top-level functions numpy,``numpy.fft``, numpy.random,
- numpy.linalg
- A selection of other useful functions and modules from matplotlib
There is no magic, and to see for yourself do
import matplotlib.pylab
matplotlib.pylab?? # prints the source code!!
When you do ipython --pylab it (essentially) just does:
from pylab import *
In a lot of documentation examples you will see code like:
import matplotlib.pyplot as plt # set plt as alias for matplotlib.pyplot
plt.plot([1,2], [3,4])
This is good practice for writing scripts and programs, since it is clear that the plot command is from the matplotlib.pyplot package. We’ll adopt this alias for the examples in our course. But once you’re familiar with the commands, you can omit the plt. when plotting in the interactive ipython shell to reduce the amount of typing needed.
See Matplotlib, pylab, and pyplot: how are they related? for a more discussion on the topic.
Plotting 1-d data¶
The matplotlib tutorial on Pyplot (Copyright (c) 2002-2009 John D. Hunter; All Rights Reserved and license) is an excellent introduction to basic 1-d plotting. The content below has been adapted from the pyplot tutorial source with some changes and the addition of exercises.
matplotlib.pyplot is a collection of command style functions that make matplotlib work like MATLAB. Each pyplot function makes some change to a figure: eg, create a figure, create a plotting area in a figure, plot some lines in a plotting area, decorate the plot with labels, etc.... matplotlib.pyplot is stateful, in that it keeps track of the current figure and plotting area, and the plotting functions are directed to the current axes:
plt.figure() # Make a new figure window
plt.plot([1,2,3,4])
plt.ylabel('some numbers')
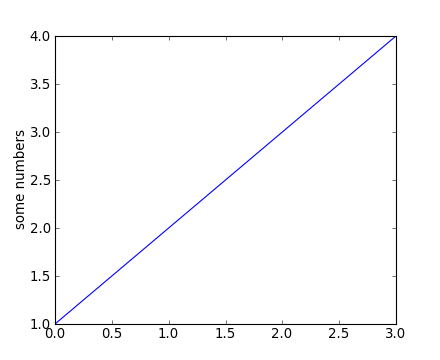
You may be wondering why the x-axis ranges from 0-3 and the y-axis from 1-4. If you provide a single list or array to the plot() command, matplotlib assumes it is a sequence of y values, and automatically generates the x values for you. Since python ranges start with 0, the default x vector has the same length as y but starts with 0. Hence the x data are [0, 1, 2, 3].
plot() is a versatile command, and will take an arbitrary number of arguments. For example, to plot x versus y, you can issue the command:
plt.clf() # this clears the existing figure
plt.plot([1,2,3,4], [1,4,9,16])
plot() is just the tip of the iceberg for plotting commands and you should study the page of matplotlib screenshots to get a better picture.
For every x, y pair of arguments, there is an optional third argument which is the format string that indicates the color and line type of the plot. The letters and symbols of the format string are from MATLAB, and you concatenate a color string with a line style string. The default format string is ‘b-‘, which is a solid blue line. For example, to plot the above with red circles, you would issue:
plt.clf()
plt.plot([1,2,3,4], [1,4,9,16], 'ro')
plt.axis([0, 6, 0, 20])
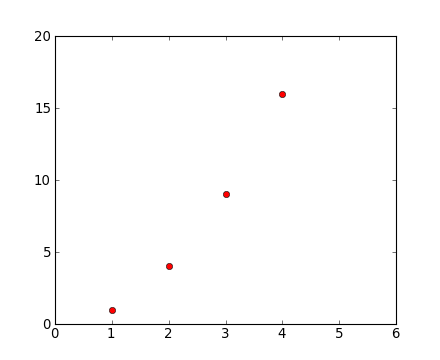
See the plot() documentation for a complete list of line styles and format strings. The axis() command in the example above takes a list of [xmin, xmax, ymin, ymax] and specifies the viewport of the axes.
If matplotlib were limited to working with lists, it would be of limited use for numeric processing. Generally, you will use NumPy arrays. In fact, all sequences are converted to numpy arrays internally. The example below illustrates plotting several lines with different format styles in one command using arrays:
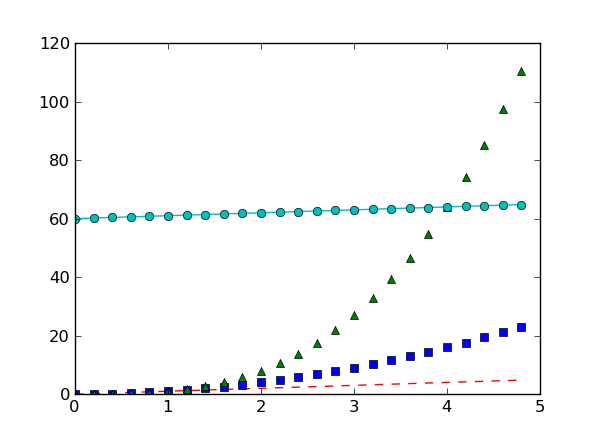
# evenly sampled time at 200ms intervals
t = np.arange(0., 5., 0.2)
# red dashes, blue squares and green triangles
# then filled circle with connecting line
plt.clf()
plt.plot(t, t, 'r--', t, t**2, 'bs', t, t**3, 'g^')
plt.plot(t, t+60, 'co-')
Exercise: Plot a sine curve
Make a plot of a sin curve between 0 and 4*pi shown by a green curve. Remember that the value of pi and the sine function are in the numpy namespace (np.pi and np.sin).
Click to Show/Hide Solution
plt.clf()
x = np.linspace(0, 4*np.pi, 100)
plt.plot(x, np.sin(x), 'g')
plt.xlim(0, 4*np.pi)
plt.ylim(-1.1, 1.1)
Controlling line properties¶
What are lines and markers?
A matplotlib “line” is an object containing a set of points and various attributes describing how to draw those points. The points are optionally drawn with “markers” and the connections between points can be drawn with various styles of line (including no connecting line at all).
Lines have many attributes that you can set: linewidth, dash style, antialiased, etc; see Line2D. There are two commonly-used ways to set line properties:
Use keyword args:
x = np.arange(0, 10, 0.25) y = np.sin(x) plt.clf() plt.plot(x, y, linewidth=4.0)
Use the setter methods of the Line2D instance. plot returns a list of lines; eg line1, line2 = plot(x1,y1,x2,x2). Below I have only one line so it is a list of length 1. I use tuple unpacking in the line, = plot(x, y, 'o') to get the first element of the list:
plt.clf() line, = plt.plot(x, y, '-') line.set_<TAB>
Now change the line color, noting that in this case you need to explicitly redraw:
line.set_color('m') # change color plt.draw()
Wait, plot() makes a plot and returns a value?
Take note that plot() both generates the plot you asked for, and returns a list of line objects. This happens for most matplotlib plotting commands. They will generate the image, contours, histogram, or whatever you want, and also return an object that you can then use to later adjust the properties of the plotted object.
Here are some of the Line2D properties.
| Property | Value Type |
|---|---|
| alpha | a float that controls the opacity |
| antialiased or aa | [True | False] |
| color or c | any matplotlib color |
| dash_capstyle | [‘butt’ | ‘round’ | ‘projecting’] |
| dash_joinstyle | [‘miter’ | ‘round’ | ‘bevel’] |
| dashes | sequence of on/off ink in points |
| data | (array xdata, array ydata) |
| figure | The figure in which the plot was made |
| label | a string used for the legend (see below) |
| linestyle or ls | [ ‘-‘ | ‘–’ | ‘-.’ | ‘:’ | ‘steps’ | ...] |
| linewidth or lw | float value in points |
| lod | [True | False] |
| marker | [ ‘+’ | ‘,’ | ‘.’ | ‘1’ | ‘2’ | ‘3’ | ‘4’ | ... ] |
| markeredgecolor or mec | any matplotlib color |
| markeredgewidth or mew | float value in points |
| markerfacecolor or mfc | any matplotlib color |
| markersize or ms | float |
| markevery | None | integer | (startind, stride) |
| solid_capstyle | [‘butt’ | ‘round’ | ‘projecting’] |
| solid_joinstyle | [‘miter’ | ‘round’ | ‘bevel’] |
| visible | [True | False] |
| xdata | array |
| ydata | array |
| zorder | a number determining the plot order (controls overlaps) |
Exercise: Make this plot

Make a plot that looks similar to the one above. You should be able to do this just by using the format string and keyword arguments to adjust the line and marker properties.
Click to Show/Hide Solution
x = [1, 2, 3, 4]
y = [3, 2, 3, 1]
plt.clf()
plt.plot(x, y, '--', linewidth=10)
plt.plot(x, y, '*r', markeredgecolor='b', markeredgewidth=5, markersize=40)
plt.xlim(0, 5)
plt.ylim(0, 4)
Some useful functions for controlling plotting¶
Here are a few useful matplotlib.pyplot functions:
| figure() | Make new figure frame (accepts figsize=(width,height) in inches) |
| clf() | Clear an existing figure |
| axis() | Set plot axis limits or set aspect ratio (plus more) |
| subplots_adjust() | Adjust the spacing around subplots (fix clipped labels etc) |
| xlim(), ylim(), axis() | Set x and y axis limits |
| xticks(), yticks() | Set x and y axis ticks |
| savefig() | Save a figure as png, pdf, ps, svg, jpg, ... |
Working with multiple figures and axes¶
MATLAB, and matplotlib.pyplot, have the concept of the current figure and the current axes. All plotting commands apply to the current axes. The function gca() returns the current axes (a matplotlib.axes.Axes instance), and gcf() returns the current figure (matplotlib.figure.Figure instance). Normally, you don’t have to worry about this, because it is all taken care of behind the scenes. Below is a script to create two figures where the first figure has two subplots:
def f(t):
"""Python function to calculate a decaying sinusoid"""
val = np.exp(-t) * np.cos(2*pi*t)
return val
t1 = np.arange(0.0, 5.0, 0.1)
t2 = np.arange(0.0, 5.0, 0.02)
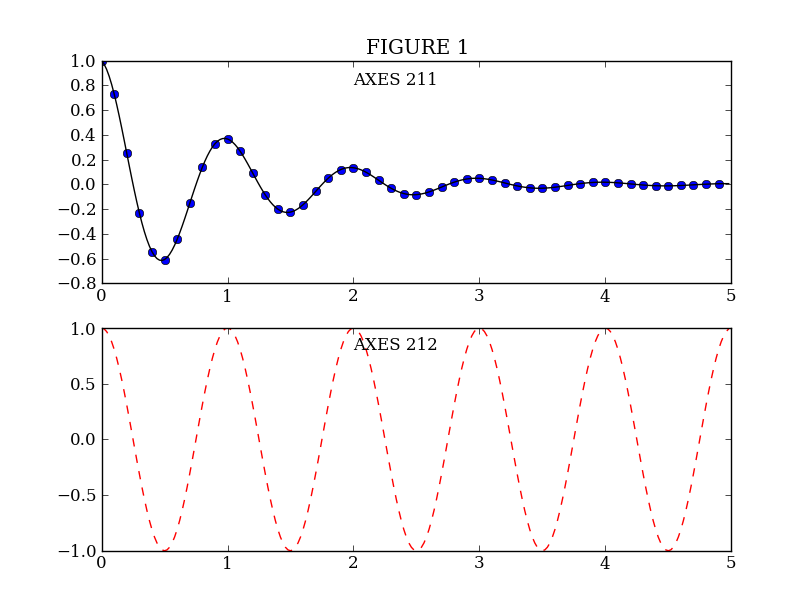
plt.figure(1) # Make the first figure
plt.clf()
plt.subplot(211) # 2 rows, 1 column, plot 1
plt.plot(t1, f(t1), 'bo', t2, f(t2), 'k')
plt.title('FIGURE 1')
plt.text(2, 0.8, 'AXES 211')
plt.subplot(212) # 2 rows, 1 column, plot 2
plt.plot(t2, np.cos(2*pi*t2), 'r--')
plt.text(2, 0.8, 'AXES 212')
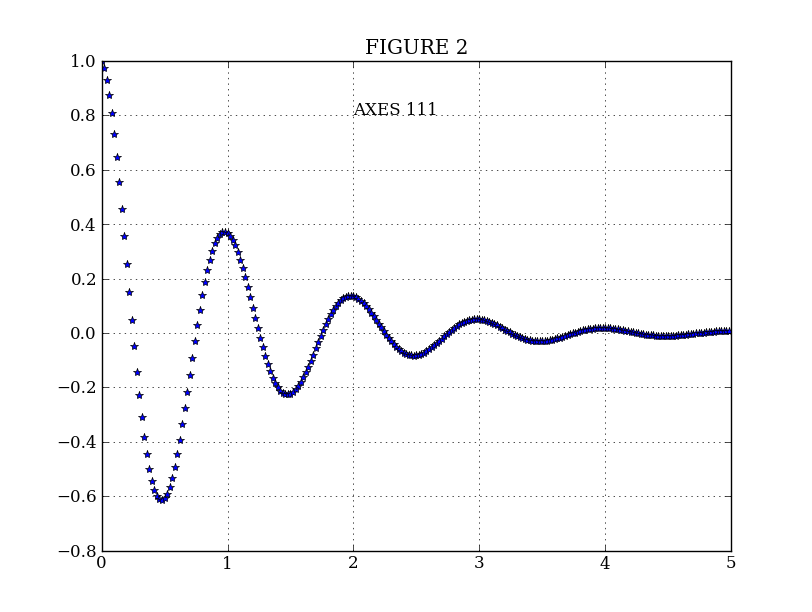
plt.figure(2) # Make a second figure
plt.clf()
plt.plot(t2, f(t2), '*')
plt.grid()
plt.title('FIGURE 2')
plt.text(2, 0.8, 'AXES 111')
Now return the second plot in the first figure and update it:
plt.figure(1) # Select the existing first figure
plt.subplot(212) # Select the existing subplot 212
plt.plot(t2, np.cos(pi*t2), 'g--') # Add a plot to the axes
plt.text(2, -0.8, 'Back to AXES 212')
|
|
The first figure() command here is optional because figure(1) will be created by default, just as a subplot(111) will be created by default if you don’t manually specify an axes.
The subplot() command specifies numrows, numcols, fignum where fignum ranges from 1 to numrows*numcols. The commas in the subplot command are optional if numrows*numcols<10. So subplot(211) is identical to subplot(2,1,1). You can create an arbitrary number of subplots and axes.
If you want to place an axes manually, ie, not on a rectangular grid, use the axes() command, which allows you to specify the location as axes([left, bottom, width, height]) where all values are in fractional (0 to 1) coordinates. See pylab_examples-axes_demo for an example of placing axes manually and pylab_examples-line_styles for an example with lots-o-subplots.
You can clear the current figure with clf() and the current axes with cla(). There is also an object oriented API which you can use instead (see the artist tutorial).Briefly, subplot and axes have equivalents that are methods of a figure; figure().add_subplot() and figure().add_axes(). In scripts it is often more convenient to use these as it makes explicit which figure the plot will appear on.
Text, Histograms and Legends¶
The text() command can be used to add text in an arbitrary location, and the xlabel(), ylabel() and title() are used to add text in the indicated locations (see the text intro for a more detailed example). Here we’ll create a histogram from some data using the hist() command and then annotate it with some text:
mu, sigma = 0, 1
x = np.random.normal(mu, sigma, size=10000)
plt.clf()
# the histogram of the data
histvals, binvals, patches = plt.hist(
x, bins=50, normed=1, facecolor='g', alpha=0.75, label='my data')
plt.xlabel('x')
plt.ylabel('Probability')
plt.title('Gaussian distribution')
plt.text(-2, 0.45, r'$\mu=0,\ \sigma=1$')
plt.xlim(-4, 4)
plt.ylim(0, 0.5)
plt.grid(True)
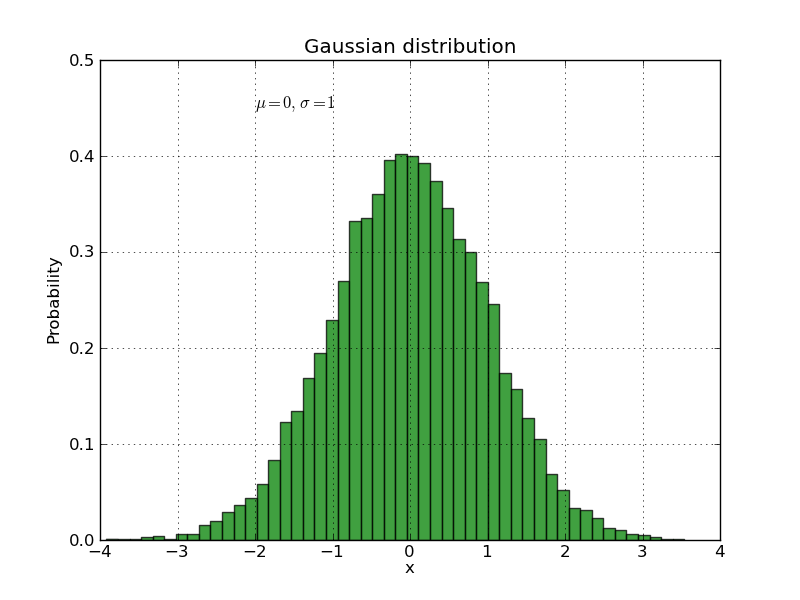
All of the text() commands return a matplotlib.text.Text instance. Just as with with lines above, you can customize the properties by passing keyword arguments into the text functions or using set_ methods:
t = plt.xlabel('my data', fontsize=14, color='red')
These properties are covered in more detail in text-properties. For example, you can change the alignment of the text with respect to the coordinates with the verticalalignment and horizontal alignment (or va and ha) keywords:
plt.text(-2, 0.45, r'$\mu=0,\ \sigma=1$', ha='right', color='g')
We’ve also added an extra keyword label to the hist() call. This will be used to label the curve if we later decide to add a legend. Let’s do that now using legend():
plt.legend(loc='best')
Type plt.legend? and take a look at the different keyword options that let you customise the legend. loc=’best’ means it will magically choose a location to minimise overlap with the plotted data.
Click to Show/Hide Solution
plt.clf()
x2 = np.random.normal(1, 1, size=10000)
bins = np.arange(-4, 5, 0.2)
out = plt.hist(x, bins=bins, normed=1, facecolor='g', alpha=0.5,
histtype='stepfilled', label=r'$\mu=0,\ \sigma=1$')
out = plt.hist(x2, bins=bins, normed=1, facecolor='r', alpha=0.5,
histtype='stepfilled', label=r'$\mu=1,\ \sigma=1$')
plt.legend(loc='best')
Using mathematical expressions in text¶
matplotlib accepts TeX equation expressions in any text expression.
For example, to write the expression 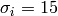 in the title
you can write a TeX expression surrounded by dollar signs:
in the title
you can write a TeX expression surrounded by dollar signs:
plt.title(r'$\sigma_i=15$')
The r preceeding the title string is important – it signifies that the string is a raw string and not to treate backslashes as python escapes. matplotlib has a built-in TeX expression parser and layout engine, and ships its own math fonts – for details see the mathtext-tutorial. Thus you can use mathematical text across platforms without requiring a TeX installation. For those who have LaTeX and dvipng installed, you can also use LaTeX to format your text and incorporate the output directly into your display figures or saved postscript – see the usetex-tutorial.
Annotating text¶
The uses of the basic text() command above place text at an arbitrary position on the Axes. A common use case of text is to annotate some feature of the plot, and the annotate() method provides helper functionality to make annotations easy. In an annotation, there are two points to consider: the location being annotated represented by the argument xy and the location of the text xytext. Both of these arguments are (x,y) tuples:
plt.clf()
t = np.arange(0.0, 5.0, 0.01)
s = np.cos(2*pi*t)
lines = plt.plot(t, s, lw=2)
plt.annotate('Local maximum', xy=(2, 1), xytext=(3, 1.5),
arrowprops=dict(facecolor='black', shrink=0.05, width=2))
plt.ylim(-2,2)
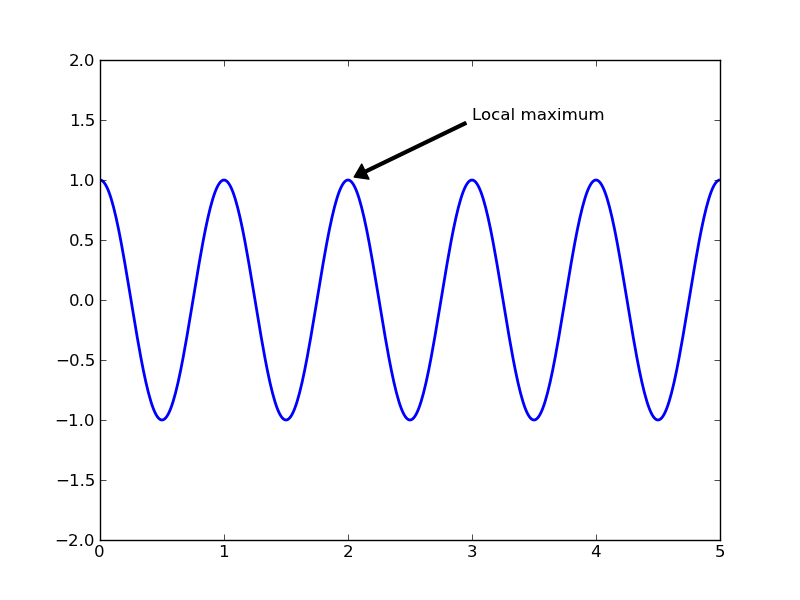
In this basic example, both the xy (arrow tip) and xytext locations (text location) are in data coordinates. There are a variety of other coordinate systems one can choose – see the annotations tutorial. More examples can be found here
Making contour plots and saving figures¶
Contour plots can be made using the contour() command, and they can then be labelled with clabel():
def gaussian_2d(x, y, x0, y0, xsig, ysig):
return np.exp(-0.5*(((x-x0) / xsig)**2 + ((y-y0) / ysig)**2))
delta = 0.025
x = np.arange(-3.0, 3.0, delta)
y = np.arange(-2.0, 2.0, delta)
X, Y = np.meshgrid(x, y)
Z1 = gaussian_2d(X, Y, 0., 0., 1., 1.)
Z2 = gaussian_2d(X, Y, 1., 1., 1.5, 0.5)
# difference of Gaussians
Z = 10.0 * (Z2 - Z1)
# Create a contour plot with labels using default colors. The
# inline argument to clabel will control whether the labels are draw
# over the line segments of the contour, removing the lines beneath
# the label
plt.clf()
CS = plt.contour(X, Y, Z)
plt.clabel(CS, inline=1, fontsize=10)
plt.title('Simplest default with labels')
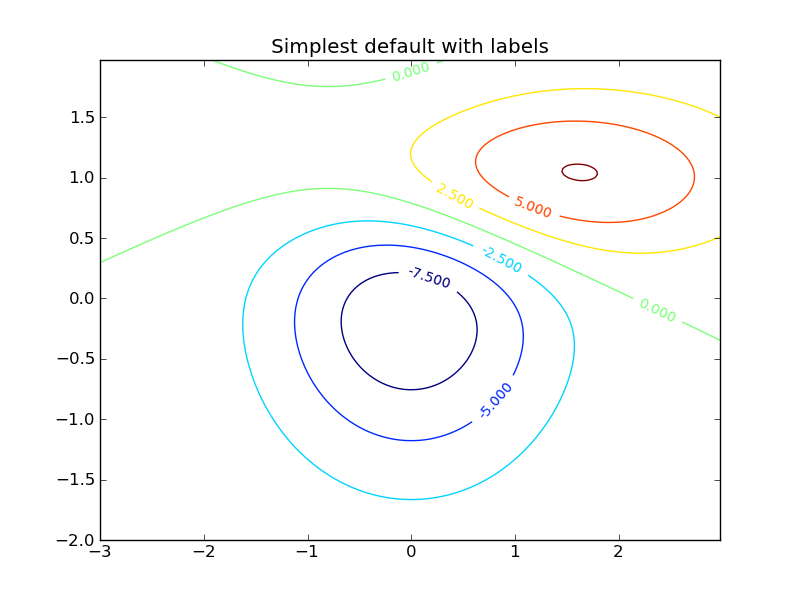
Once you’ve made plots, they can be saved with savefig. They can be saved as jpg, png, pdf, ps, svg and other formats; the format is inferred from the suffix of the filename:
plt.savefig('contour.pdf')
png format is generally best for putting in talks. For papers and posters it’s better to use a vector format like ps, pdf or svg. There can be small differences between the plot you see on the screen and a saved pdf or ps version, so check the saved version looks as you expect. (Often the saved vector format version will look better!)
You can also save a plot using the button in the plotting window.
Exercise: Make a contour plot
Make a contour plot of a single 2d gaussian centred on 0,0. You should show only 2 contours that are both coloured black. Label the inner contour with ‘99%’ and the outer contour with ‘95%’. You might want to take a look at the fmt keyword in the help for clabel() to see how to give your own contour labels, and take note that the values of each contour level are stored in CS.levels.
Click to Show/Hide Solution
x = np.linspace(-2.0, 2.0)
y = np.linspace(-2.0, 2.0)
X, Y = np.meshgrid(x, y)
Z = gaussian_2d(X, Y, 0, 0, 1., 1.)
plt.figure()
CS = plt.contour(X, Y, Z, 2, colors='k')
fmt = {CS.levels[0]: '95%', CS.levels[1]: '99%'}
plt.clabel(CS, fmt=fmt)
Other 2-d plots¶
A deeper tutorial on plotting 2-d image data will have to wait for another day:
- To plot images take a look at at the image tutorial
- APLpy allows you to easily make publication quality images for astronomical fits images incorporating WCS information.
Plotting 3-d data¶
Matplotlib supports plotting 3-d data through the mpl_toolkits.mplot3d module. Let’s take a look at an example of the 3-d viewer that is available:
from mpl_toolkits.mplot3d import Axes3D
import numpy as np
import matplotlib.pyplot as plt
def gaussian_2d(x, y):
return np.exp(-0.5*(x**2 + y**2))
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
vals = np.linspace(-3, 3)
x,y = np.meshgrid(vals, vals)
z = gaussian_2d(x, y)
ax.plot_wireframe(x, y, z, color='0.3', lw=0.5)
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
To get more information check out the mplot3d tutorial.
Putting it all together¶
Let’s use some of what we’ve learned over the past few lessons to plot a 2d distribution, overlay some contours, and show the 1d histograms corresponding to each dimension. You should understand everything that’s going on here - if you don’t, please ask!:
# the random data
x = np.random.randn(1e5)
y = np.random.randn(1e5)
# start with a rectangular figure
plt.figure(figsize=(6, 6))
# define the axes positions
left = bottom = 0.1
width = height = 0.7
ax_main = plt.axes([left, bottom, width, height])
ax_top = plt.axes([left, bottom + height, width, 0.15])
ax_right = plt.axes([left + width, bottom, 0.15, height])
# plot the data points
ax_main.plot(x, y, '.', markersize=0.5)
# now let's overplot some contours. First we have to make a 2d
# histogram of the point distribution.
vals, xedges, yedges = np.histogram2d(x, y, bins=30)
# Now we have the bin edges, but we want to find the bin centres to
# plot the contour positions - they're half way between the edges:
xbins = 0.5 * (xedges[:-1] + xedges[1:])
ybins = 0.5 * (yedges[:-1] + yedges[1:])
# now plot the contours
ax_main.contour(xbins, ybins, vals.T, 4, colors='k', zorder=10)
# finally plot 1d histograms for the top and right axes.
bins = np.arange(-3, 3.1, 0.1)
ax_top.hist(x, bins=bins, histtype='stepfilled')
ax_right.hist(y, bins=bins, orientation='horizontal', histtype='stepfilled')
# make all the limits consistent
ax_top.set_xlim(-3, 3)
ax_right.set_ylim(-3, 3)
ax_main.set_xlim(-3, 3)
ax_main.set_ylim(-3, 3)
# remove the tick labels for the top and right axes.
ax_top.set_xticklabels([])
ax_top.set_yticklabels([])
ax_right.set_xticklabels([])
ax_right.set_yticklabels([])
plt.draw()